在现有的桥梁健康监测系统，尤其是大跨径的桥梁的健康监测系统中，用于采集数据的传感器多达几百甚至上千个，有各种不同类型并且分布在桥梁的不同测点，它们按照指定的策略获取桥梁的响应信息，为桥梁结构健康状态分析和评估提供数据基础。在后续的桥梁健康监测数据分析中，由于存在众多的传感器类型和测点，如果不考虑不同数据之间的关联性，不但会增加分析过程的复杂度还可能给分析结果带来偏差，因此有必要对不同测点数据之间的关联性以及不同类型传感器数据之间的关联性进行分析。

1 温度与应变关联性

对温度数据与应变数据的关联性进行研究，首先需要对数据的特征、数据的分布、数据的变化趋势以及数据之间的相关关系等进行观察和分析；然后通过计算相关系数等定量指标来确定数据之间相关性的强弱以及相关的方向；最后使用对应的分析模型对数据进行拟合，得出相应的拟合参数。

本文对温度与应变的关联性分析的步骤如下：

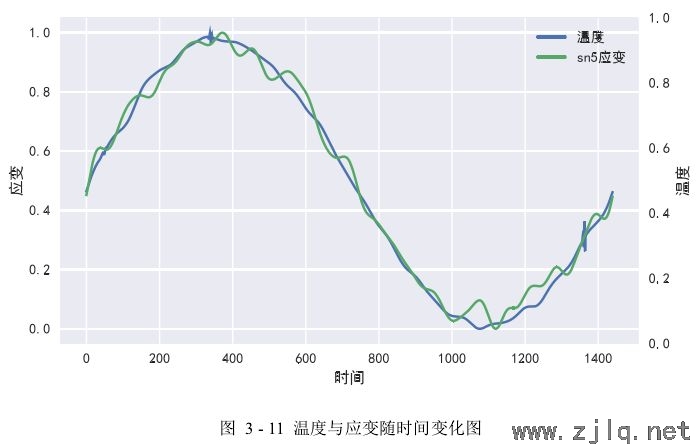
1）首先将温度数据和应变数据放在同一个折线图中进行观察，折线图呈现的是数据随时间变化的趋势，其中横坐标是时间，两个纵坐标分别是应变和温度。如图3-11所示是𝐷 = [63,0.5]的sn5测点应变数据与底板温度数据随时间变化的折线图，从图中可以看出：a）经过数据标准化操作之后，应变数据和温度数据的数值都落在[0,1]之间；b）经过异常值处理和噪声去除操作后，温度曲线与应变曲线变得更加平滑；c）数据标准化之后，温度曲线整体呈正弦变化趋势，应变曲线整体上也呈现正弦变化趋势，且应变曲线变化趋势和温度曲线变化趋势基本一致。对其他测点的应变数据与温度数据进行观察，能够得到类似的结果，这表明桥梁健康监测数据中的应变与温度数据之间的相关程度较高，也说明在众多影响应变的因素中，温度是最主要的因素。

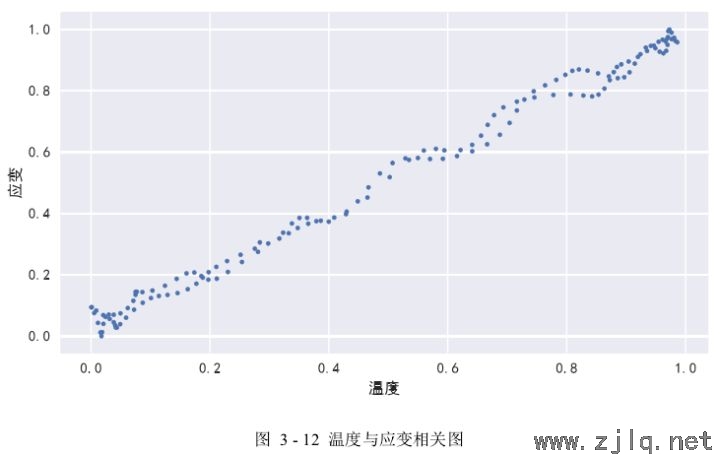
2）接下来使用相关图对它们的相关形式、方向和密切程度进行大致判断。如图3-12 所示是𝐷 = [63,0.5]的 sn5 测点应变数据与底板温度数据的相关图，去除了时间维度的影响，只关注温度与应变两组数据之间的关系，其中温度作为自变量放在横坐标，应变作为因变量放在纵坐标。从图中可以看出，温度与应变具有相同的变化趋势，当温度增加时应变也相应增加，且二者对应的坐标点近似于分布在一条直线周围，这表明温度与应变呈现线性关系，并且根据坐标点的离散程度来看，它们具有较强的线性相关性。

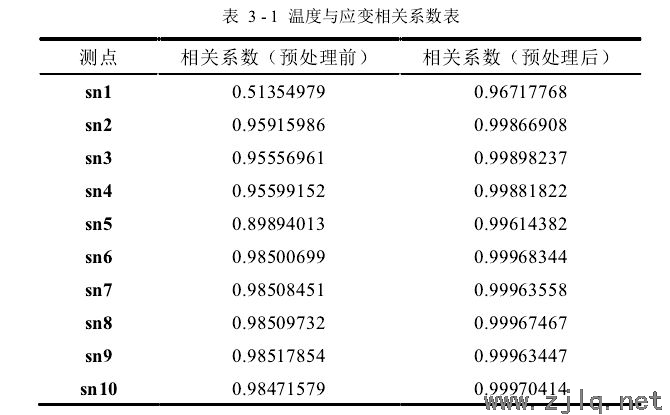
3）从前面步骤可以得出温度与应变具有较强的线性相关性，这个线性相关性的强弱可以使用相关系数来衡量，相关系数是用来反映变量之间相关性强弱的统计指标，其取值范围是[−1,1]。如表3-1所示是工况𝐷 = [63,0.5]下 10 个测点的应变数据与温度数据的相关系数表，从表中可以看出：a）预处理前和预处理后的相关系数都为正值，说明温度与应变呈正相关关系；b）预处理后的相关系数基本都接近 0.99，根据相关系数绝对值越接近 1，相关性越强，说明预处理后的应变数据与温度数据具有非常强的线性相关性；c）预处理后相关系数比预处理前的相关系数大，可见预处理后的应变数据与温度数据的相关性变强，预处理提升了两者之间的相关性，说明预处理操作在本文的数据分析中起到重要作用。

4）对于具有线性相关性的自变量和因变量，使用一元线性回归模型进行分析，其数学表示形式为：

𝑦 = 𝛼𝑥 + 𝛽 （1）

其中y是因变量，x是自变量，𝛼是回归系数，𝛽是常数项。要确定y与x之间的定量关系，需要确定𝛼与𝛽的值，通常使用最小二乘法或者梯度下降法来进行求解。而对于线性模型对数据的拟合程度，本文使用均方根误差（Root Mean Squared Error，RMSE）来进行衡量，RMSE 是模型估计值与数据真实值之差的平方的期望值的算术平方根，RMSE 的计算公式如下：

（2）

其中𝑓𝑖表示模型估计值，𝑦𝑖表示数据真实值。均方根误差可以衡量模型对数据的拟合程度，RMSE 数值越小说明拟合越好。以𝐷=[63,0.5]的sn5测点应变数据为例，使用一元线性回归模型进行拟合分析，其中温度数据作为自变量x，应变数据作为因变量y，对模型进行求解可得到𝛼=0.96420992，𝛽=0.02618689，因此温度与应变的一元线性回归模型数学表示形式为：y=0.96420992x+0.02618689，该次拟合的均方根误差为 0.029325，说明拟合程度较高。

5）最后对所有测点进行线性回归拟合，并计算其均方根误差。如表3-2所示是10 个测点应变数据与温度数据拟合得到的回归系数𝛼及常数项𝛽，以及对应的均方根误差 RMSE。从表中数据可以看出 sn6-sn10 的拟合程度较高，sn1 的拟合程度最低，说明sn6-sn10 测点的温度与应变的线性相关性较强，sn1 测点的温度与应变相关性相对较弱。

上述实验可以得出：1）sn1~sn10 测点的温度数据与应变数据都存在强线性相关性；2）这些测点的温度数据与应变数据能够使用线性回归模型进行拟合，得到相应的回归系数和常数项。

2 不同测点应变关联性

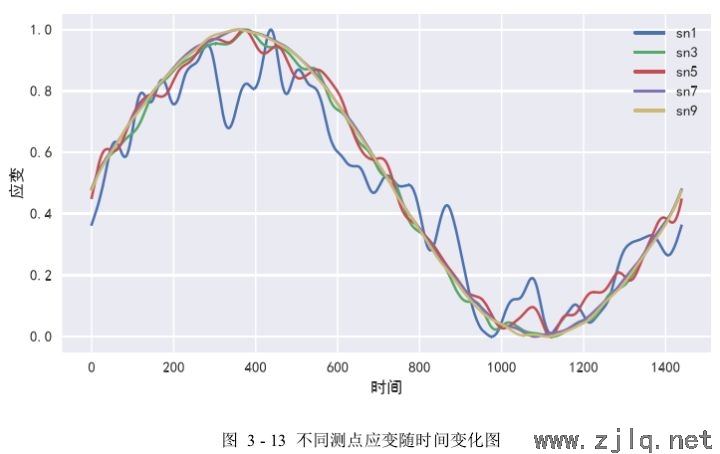
对不同测点之间的应变数据进行关联性研究，首先需要对不同测点的应变数据进行定性观察与分析。如图3-13所示实验中，从工况𝐷=[63,0.5]的所有测点中选5个测点：sn1、sn3、sn5、sn7、sn9，对这些测点应变数据随时间变化的趋势进行观察，从图中可以看出五个测点的应变数据整体变化趋势是一致的，都是呈正弦曲线变化，其中sn1测点和sn5测点的应变曲线波动幅度较大，而其他测点的应变曲线较平稳，由此可以说明不同测点的应变数据之间存在较强的相关性，但sn1测点、sn5测点与其他测点的相关性相对而言弱一些。

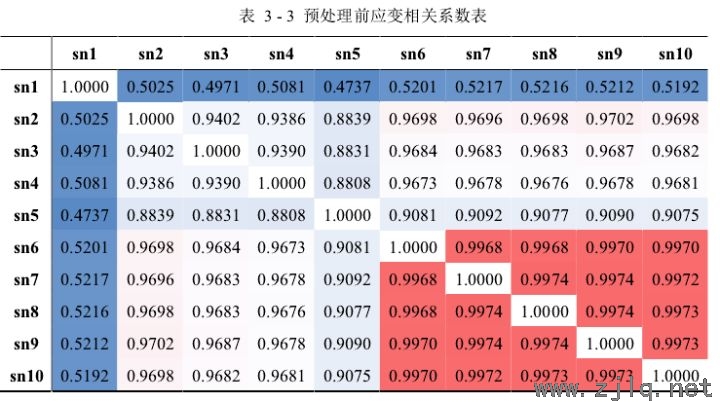
接下来对定性的观察结果做进一步的分析，分别计算不同测点应变数据之间的相关系数来定量地确定它们之间相关性的强弱。如表3-3和表3-4所示实验中，分别计算预处理前后的应变数据之间的相关系数，并使用相关系数矩阵进行展示，表中数据使用不同颜色进行标记，其中红色越深表示相关系数越大，相关性越强，而蓝色越深表示相关系数越小，相关性越弱。

从表 3 - 3 实验中可以得出：1）除 sn1 以外的其他测点应变数据的相关系数在 0.9以上，表明这些测点应变数据的相关性很强；2）sn6~sn10 测点应变数据间的相关系数处于红色区域，sn1~sn5 测点应变数据间的相关系数处于蓝色区域，而 sn1~sn5 是桥梁底板的测点，sn6~sn10 是桥梁顶板的测点，表明桥梁顶板应变数据间的相关性比桥梁底板应变数据之间的相关性更强。

从表3-4实验中可以得出：1）所有测点预处理后的应变数据之间的相关系数变大，表明去除异常值和噪声后的相关性变强，预处理操作对应变数据的关联性分析起了积极作用；

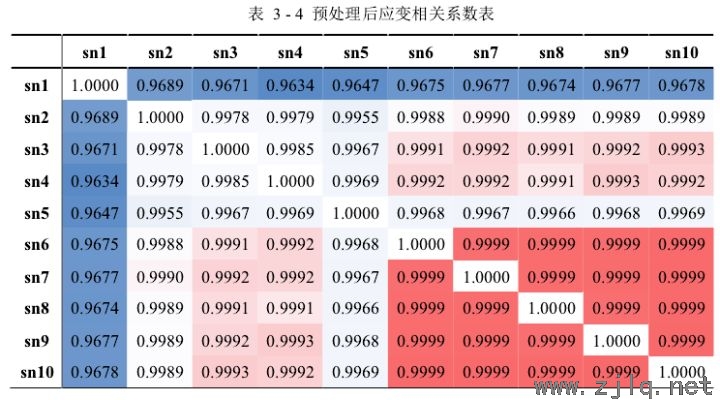
2）sn1 和 sn5 测点的应变数据与其他测点的应变数据相关系数增大到 0.96 以上，相关性大大加强，表明这两个测点的应变数据对异常值和噪声比较敏感，更容易受到外界环境的影响。